The E and Eye
Story Highlights
“HDTV is ideally viewed at a distance of roughly three times the picture height.” That’s the sort of statement heard frequently — as recently as at last week’s HPA Tech Retreat. And there seems to be a basis for it.

According to the eye chart commonly used to determine visual acuity, 20/20 vision can just identify two black lines separated by a white line that covers one minute of arc on the retina. There are 360 degrees of arc in a circle and 60 minutes per degree (and 60 seconds per minute).
If you divide the 1080 active (picture-carrying) lines of the most common form of HDTV by those 60 minutes, the result is 18 degrees of retinal angle. Divide that by two, and you can form two right triangles, one above the other. The sides opposite the 9-degree angles are each half the height of the HDTV screen. The sides adjacent to the angles are the distance from the screen to the eye.
The tangent of an angle is the ratio of the opposite side to the adjacent. The tangent of 9 degrees is roughly 0.158. Double that to include both right triangles, and the result is roughly 0.317. Divide 1 by that to get the ratio of viewing distance to height, and the result is roughly 3.16.
According to the theory of that eye chart, if you sit about 3.16 times the height of your HDTV screen away from it, you’ll get optimum resolution. Sit farther, and you’ll lose some detail. Sit closer, and you might not be able to see the picture due to the visibility of the scanning structure.
For 720-line HDTV, the viewing distance is roughly 4.76 times the height (4.76H). For old-time NTSC, it’s roughly 7.15H.
There are a few problems with this theory. One came with a slight change in this sentence: “Optimum NTSC resolution is achieved by sitting roughly seven times the picture height from the screen.” Over time, it became “People watch NTSC at roughly seven times the picture height.”
I can think of at least one person who might take out a tape measure, run some calculations, and move a chair to the optimum viewing spot. But I can’t think of many.
Bernie Lechner, then a researcher at RCA Laboratories, decided to measure how far people sat from their TVs. At the time, the result was about nine feet, regardless of screen size, a figure that became known as the Lechner Distance. Richard Jackson at Philips Laboratories in the UK came up with a similar three meters.
The Lechner/Jackson Distance was based largely on the size of living rooms and their furniture. In Japan, viewers sat closer to their TVs, thus needing HDTV. Or so the theory goes. But Japanese screen sizes also tended to be smaller.
Other problems with the optimum-viewing-distance theory relate to such issues as overscan and the reductions of vertical resolution caused by interlace, overlapping scanning lines, sampling filtering, color-phosphor dots or stripes, and CRT faceplate optical characteristics. But a much more serious issue is that one arc minute derived from the eye chart.
Officially, that eye chart (shown near the top of this post) is called a Snellen chart, named for the Dutch ophthalmologist who introduced its symbols in 1862. And the symbols on it are said not to be letters in a typeface but “optotypes” intended to identify visual acuity.
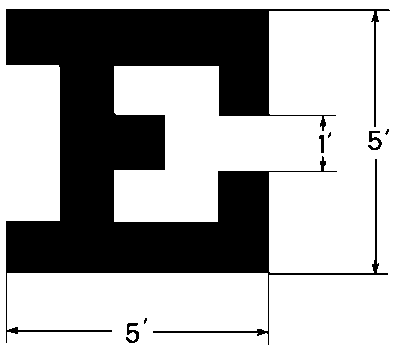 Consider the famous E. When it is located on the 20/20 line of “normal” vision (meaning that the viewer sees at 20 feet what should be just visible at 20 feet — or, outside the United States, the 6/6 line, meaning the viewer sees at six meters what should be just visible at six meters), the entire symbol fits within an arc that subtends a retinal angle of 5 minutes (5/60 of a degree), and each black or white feature of the symbol is 1 minute.
Consider the famous E. When it is located on the 20/20 line of “normal” vision (meaning that the viewer sees at 20 feet what should be just visible at 20 feet — or, outside the United States, the 6/6 line, meaning the viewer sees at six meters what should be just visible at six meters), the entire symbol fits within an arc that subtends a retinal angle of 5 minutes (5/60 of a degree), and each black or white feature of the symbol is 1 minute.
That’s it. That’s the basis for viewing HDTV at three times the picture height. But maybe it’s worth examining that basis somewhat further.
First, 20/20 is not the lowest line on a typical Snellen eye chart. Here’s what the Snellen obituary on page 296 of the February 1, 1908 issue of the British Medical Journal had to say about it:
“He started with the idea that a person might be considered to have normal vision if he could see and distinguish a letter which subtended an angle of one minute on the retina. This was by no means the best which most eyes could do, but he set this as the minimum standard required to justify one in regarding an eye as normal.”
 So viewers could conceivably view HDTVs from farther away and still see full resolution. And then there are two issues I’ve raised in previous posts.
So viewers could conceivably view HDTVs from farther away and still see full resolution. And then there are two issues I’ve raised in previous posts.
One is contrast (see Angry About Contrast here: http://schubincafe.com/blog/2009/09/angry-about-contrast/). The portion of a Pelli-Robson chart pictured here shows how important contrast is in being able to distinguish symbols. TV pictures, whether NTSC or HDTV, tend to comprise a broad range of contrast ratios, and so do the screens on which they’re viewed (and the environments in which that viewing is done; the light of a lamp reflected off a screen can wreak havoc with contrast).
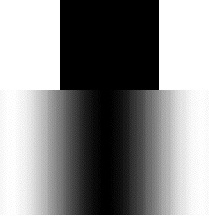 The other issue I’ve gone into before is edges (see Sines of the Times here: http://schubincafe.com/blog/2009/12/sines-of-the-times/). The E on a Snellen chart has nice sharp edges. Making sharp edges requires harmonics far beyond the fundamental sine-wave frequency. Compare the sharp-edged line at top left with the more sinusoidal line below.
The other issue I’ve gone into before is edges (see Sines of the Times here: http://schubincafe.com/blog/2009/12/sines-of-the-times/). The E on a Snellen chart has nice sharp edges. Making sharp edges requires harmonics far beyond the fundamental sine-wave frequency. Compare the sharp-edged line at top left with the more sinusoidal line below.
One arc minute of visual acuity is the same as 30 cycles per degree (a cycle comprising both a light part and a dark part). And that figure has become etched in stone for some who discuss visual resolution. But then there was the paper “Research on Human Factors in UHDTV,” published in the April 2008 SMPTE Journal by authors at NHK, the Japan Broadcasting Corporation, source of modern HDTV.
It noted that observers could tell the difference between 78 cycles per degree (cpd) and 156. The latter figure is more than five times greater than the 30 cpd of 20/20 vision. Further, the research found that the sensation of “realness” rises rapidly to 50 cpd but continues rising to 156 (with no indication that it stops there).
So, how fine is visual acuity for detail perception? I don’t know. But it doesn’t seem to be a simple 30 cpd.
